Before we learn about composite numbers, let us first try to understand whole numbers, prime numbers, and factors to a whole number. Once we know these concepts, you can easily find composite numbers.
1) Whole numbers –
Whole numbers are a set of positive integers, including the number zero. Therefore, they are also part of real numbers but does not include fractions and decimals. They are just the counting numbers that we use daily.
Example of Whole Numbers – 0, 2, 3, 6,11, 23, 45, 67, 98, 100 etc.
2) Factors to a Whole number –
Factors of a whole number divide the number so that it does not give any remainder, i.e. remainder is zero. Therefore, if we assume 6 as a whole number, its factors are 1, 2, 3, and 6 itself.
3) Prime Numbers –
Prime numbers are a set of whole numbers greater than 1, and that has only two factors, the number itself and 1.
So, prime numbers between the whole numbers 0 to 6 are 3 and 5. The numbers 3 and 5 have only two factors, the numbers themselves and 1.
Also Read: How To Score Well In IMO Along With Class 10
Composite Numbers –
What are Composite Numbers then?
Well, all the whole numbers except 0, 1 and prime numbers are composite numbers. It is an easy deduction from all the concepts that we have learned so far. However, the proper definition of composite numbers is given below.
Composite numbers are whole numbers with more than two factors, including the 1 and the number itself. That means composite should have at least more than two factors.
Let us refer back to the previous example given above. The number 6 is composite since it has 4 factors, i.e. 1, 2, 3, 6.
We should also remember that the number 1 is neither a prime nor composite.
Composite Numbers List from 1 to 100
Now, let us look at the below picture that lists the composite number from 0 to 100.
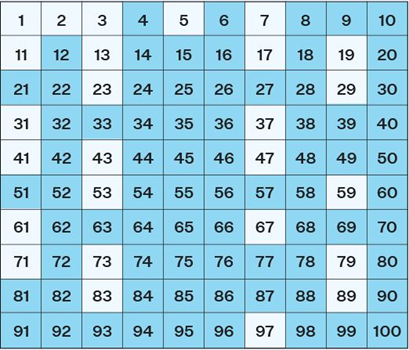
As we can see from the above picture that there are 74 composite numbers between 0 and 100. The composite numbers are given in the boxes with a blue colour background. We can also deduce that there are 25 prime numbers in the same range (excluding the numbers 0 and 1).
Difference between Composite Numbers and Prime Numbers –
As we have learnt about prime numbers and composite numbers in the above explanation. Let us now try to find the differences between them. The points of difference are thus given below –
- Prime numbers are divisible only by the number 1 and the number itself. However, for a composite number, it is divisible by at least three factors. These include the number 1 and the number itself, along with another one or more factors.
- Prime numbers are known as a product of only two numbers. However, a composite number can be a product of two or more numbers or factors.
Even and Odd Composite Numbers –
Before we learn about the next concept, let us understand what even and odd numbers are.
1) Even Numbers –
Even numbers are integers that can be divided into two equal groups of numbers. In other words, even numbers are divisible by 2 and leave no remainder, i.e. remainder is zero.
For example – The number 10 can be easily divided into two groups of numbers 5 and 5. Similarly, the number 44 can be equally divided into two groups, 22 and 22. This is the same for the numbers 4, 6, 8, 10, etc.
2) Odd Numbers –
Odd numbers are not divisible by 2 and always leaves a remainder of 1 when divided by the number 2.
For example – The numbers 3, 5, 7, 11, 13 are all odd.
So, what are odd and even composite numbers?
Since we now know the concept of prime numbers, composite numbers, odd and even numbers, we can easily deduce odd and even composite numbers. So, we know for a fact that they can’t be 0, 1, and prime numbers. So, after understanding the concept of even and odd integers, let us go through the next concept.
3) Odd Composite Numbers –
Odd composite numbers are those odd whole numbers (not divisible by 2, except 1 and 0) that are not prime numbers. So, from the previous group of numbers ranging from 0 to 100, there were 74 composite numbers. Out of these numbers, the odd composite numbers are –
9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95, 99.
4) Even Composite Numbers –
Even composite numbers are those even whole numbers (divisible by 2) that are not prime numbers. So, the even composite numbers are –
4, 6, 8, 10, 12, 14, 18, 20 etc.
Properties of Composite Numbers
Students need to keep a note and remember the following points. Students can also take notes of the following points so that they can easily recall these numbers. This is vital for scoring marks during competitive exams. The following are the properties of composite numbers-
- Composite numbers need to have more than two factors, i.e. at least three factors, including 1 and the number itself.
- The composite numbers are a factor of themselves.
- From the above example, it is clear that the smallest composite number is 4.
- When divided by their factors, composite numbers leave the remainder as zero, i.e. they are divisible by all their factors.
- All composite numbers will have at least two factors which are prime numbers.
- All the composite numbers are easily divisible by their prime or composite factors.
How to find Composite Numbers?
From the above examples and concepts, it is now easy to calculate composite numbers. One of the easiest methods to find the composite number is given below:
- First, find the factors of that particular number (Eg: Let’s take a number 6. So, the factors are 1, 2, 3, 6)
- If such a number has more than two factors or at least a minimum of three factors, including 1 and the number itself, it is a composite number. (Since 6 has more than 2 factors, therefore 6 is a composite number).
- If the number is divisible by common factors, either odd or even, it is a composite number. (6 is easily divisible by its factors 2 and 3).
Conclusion
There are several easy and quick guides available online to learn numbers and are well explained with examples. You can easily learn them by practising some examples from your NCERT or Maths books.
Computational thinking is the essential requirement for any student to use them in a real-world application gradually. Students need to have a basic understanding of numbers and numerical concepts and be polished and studied with perfection.

